
Zadanie Losy (los)
Pomóż nam usprawnić bazę zadań!
Losy
Limit pamięci: 32 MB
W pewnej szkolnej zabawie przygotowano  koszyków i do każdego z nich wrzucono pewną
liczbę losów. Niektóre z losów są wygrywające i za wylosowanie takiego losu dostaje się
prawo do opuszczenia jednej godziny lekcyjnej bez usprawiedliwienia.
koszyków i do każdego z nich wrzucono pewną
liczbę losów. Niektóre z losów są wygrywające i za wylosowanie takiego losu dostaje się
prawo do opuszczenia jednej godziny lekcyjnej bez usprawiedliwienia.
Kozik szybko obliczył, że chciałby opuścić 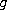 godzin w danym roku szkolnym. Powinien więc
kupić tyle losów, aby mieć pewność, że wśród wszystkich kupionych będzie co najmniej
godzin w danym roku szkolnym. Powinien więc
kupić tyle losów, aby mieć pewność, że wśród wszystkich kupionych będzie co najmniej 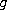 losów
wygrywających. Kozik ma jednak ograniczone fundusze, dlatego chciałby zrobić to jak
najmniejszym kosztem, czyli kupić jak najmniej losów. Zakładamy, że Kozik wie, ile jest
w każdym pojemniku losów wygrywających, a ile przegrywających.
losów
wygrywających. Kozik ma jednak ograniczone fundusze, dlatego chciałby zrobić to jak
najmniejszym kosztem, czyli kupić jak najmniej losów. Zakładamy, że Kozik wie, ile jest
w każdym pojemniku losów wygrywających, a ile przegrywających.
Wejście
Pierwszy wiersz standardowego wejścia zawiera dwie liczby całkowite  ,
, 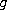 (
(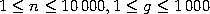 ), oznaczające odpowiednio liczbę
koszyków z losami oraz liczbę godzin, jakie chciałby opuścić Kozik.
), oznaczające odpowiednio liczbę
koszyków z losami oraz liczbę godzin, jakie chciałby opuścić Kozik.
W  kolejnych wierszach znajduje się opis kolejnych koszyków.
Każdy wiersz zawiera dwie liczby całkowite
kolejnych wierszach znajduje się opis kolejnych koszyków.
Każdy wiersz zawiera dwie liczby całkowite 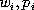 (
(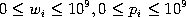 ), oznaczające odpowiednio liczbę losów wygrywających oraz
przegrywających w
), oznaczające odpowiednio liczbę losów wygrywających oraz
przegrywających w 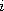 -tym koszyku.
-tym koszyku.
W testach wartych około 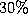 punktów zachodzi dodatkowy warunek
punktów zachodzi dodatkowy warunek 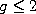 .
.
Wyjście
Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać jedną liczbę całkowitą,
równą minimalnej liczbie losów, jakie powinien kupić Kozik lub jedno słowo NIE,
gdy Kozik nie może kupić tylu losów, aby opuścić co najmniej 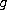 godzin.
godzin.
Przykład
Dla danych wejściowych:
4 3 2 5 0 5 2 0 2 2
poprawną odpowiedzią jest:
5
Autor zadania: Jacek Tomasiewicz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English